Kalid Azad: Calculus, Better Explained

Integrals

A cube $x^3$ has 3 components, the sides a, b, c (all equivalent to x):

• a thinks: my change ($da$) is combined with other constant sides to get $da \times b \times c$

• b and c think the same about themselves

• each change happens separately with no “crosstalk” between $da$, $db$, and $dc$.

• every side is identical ($a = b = c = x$)

• changes are the same ($da = db = dc = dx$)

• so $(dx \times x \times x) + (dx \times x \times x) + (dx \times x \times x) = x^2 \times dx + x^2 \times dx + x^2 \times dx = 3x^2 \times dx$

• $x^3$ has 3 identical perspectives

• When the system changes, all 3 perspectives contribute identically. Therefore, the derivative will be 3 × something.

• The “something” is the change in one side (dx) multiplied by the remaining sides (x × x).

  • The changing side goes from x to dx
  • and the exponent lowers by one.

$$

\begin{equation} \int x^2 \end{equation}

$$

just imagine that incoming change is being split 3 ways:

$x^2 = \frac{x^2}{3} + \frac{x^2}{3} + \frac{x^2}{3} = \frac{1}{3} 3x^2$

now we have 3 plates (each 1/3 of the original size) and we can integrate a smaller cube.

Why many different answers for integrals? Because many different possible functions. If $f’(x) = 4$, that only shows the change for each additional step, but the starting conditions could be different (the constant $+c$).

• Definite integral tracks accumulation of a set amount of slices, range can be numbers.
• Indefinite integral finds the actual formula that created the pattern of steps

Derivatives

Derivative definition:

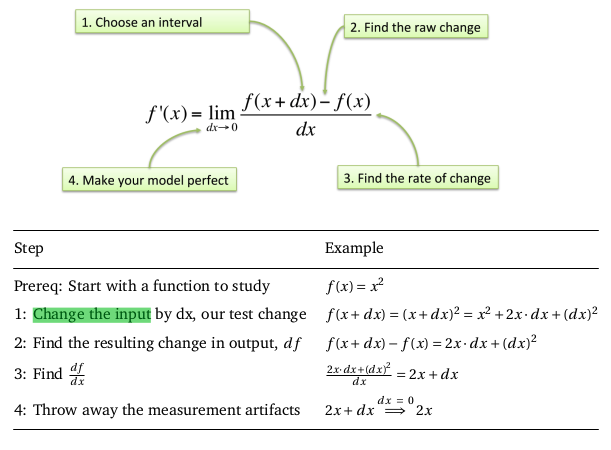
$f(x) = 4x$ is a relationship, an increase in x by 1 raises the result by 4. The steps:

1. Get current output, $f(x)$: $f(1) = 4$
2. Step forward by $dx$ (such as 1).
3. Find the new amount, $f(x + dx)$: $f(1+1) = f(2) = 8$
4. Compute the difference: $f(x + dx) - f(x) = 8 - 4 = 4$

So for $f(x) = 4x$ we have $f(x + dx) - f(x) = 4(x + dx) - 4(x) = 4dx$.

This can be expressed as a ratio:

• $dx$ is change in input
• $df$ is resulting change in output ($= f(x+dx) - f(x)$)
• $\frac{df}{dx}$ is ratio of output change to input change.

Put together:

$\frac{df}{dx} = \frac{4dx}{dx} = 4$