Linear algebra notes

Basis: linearly independent, spans subspace Linearly independent: only trivial solution. vectors are not multiples of each other Homogenous: contains zero vector, may have more solutions

standard matrix: $A = [ T(e_1) T(e_2) … T(e_n) ]$ T(x) == Ax

• ‘onto’: pivot in every row
• ‘one-to-one’: only trivial solution if = 0

Spans subspace if has solution

inverse: augment with I and reduce to get I on the left

Basis ColA: pivot cols of orig matrix (also “basis for subspace”)

Basis NulA: intersections with 0 vector in parametric form

coordinates from basis: $x₁ \overrightarrow{b_1} + x₂ \overrightarrow{b_2} + …$

eigen: $Ax = \lambda x \leftrightarrow (A - \lambda I) x = 0$

$A^n = P D^n P^{-1}$. P eigen vectors, D eigenval on diagonals

To diagonalize:

1. Eigenvalues

2. Bases for eigenvalues ($A - \lambda I$) solve

3. Write as P,D

   

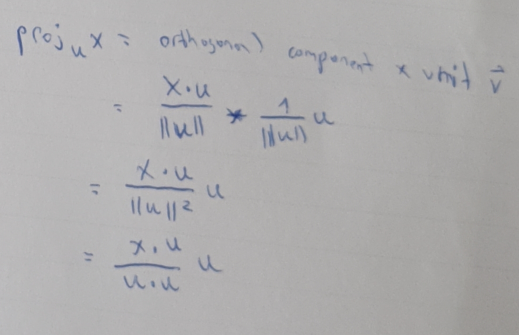
   Normalize $\rightarrow{v}: \frac{v}{|| v ||}$

   Gram-Schmidt: $v - proj_w v$

   Orthogonal: $u \dot v = 0$

   Orthonormal: set is orthogonal, $||u|| = 1$ for every u

   Characteristic polynomial: $det(A - \lambda I)$

   SVD:

   • $A = U \Sigma V^T$

   • U: eigenvectors $AA^T$

   • V: eigenvectors $A^T A$

   • D: sqrt eigenvalues descending diagonal